Water Balance in Root Zone of Soils: Theory, D.L. Nofziger
General Description Model Description Simplifications Glossary Bibliography and Contributors
Water Balance in the Root Zone
The movement and storage of water in surface soils is important for economic and environmental reasons. The ability of a soil to store water in the root zone determines its ability to support plant growth and crop production. Water moving through the root zone has the potential of carrying chemicals downward to the underlying aquifers. Rainfall and irrigation water entering the soil tends to replenish the soil storage reservoir and extend its ability to support plant life. If infiltrating water exceeds the storage capacity of the soil root zone, the excess water tends to move downward through the soil. This deep drainage contributes to recharging the aquifer below. The challenge to farm managers is to provide sufficient water for producing a crop while limiting the amount of water and dissolved chemicals moving deeply into the soil.
This software uses the water balance concept to estimate water available for plants and water drainage below the root zone. The basic concept is just a statement of the principle of conservation of mass. It can be represented by the equation
Infiltration - Evapotranspiration – Increase In Storage = Drainage
where Infiltration represents the amount of water entering the soil surface from rainfall or irrigation, Evapotranspiration represents the amount of water leaving the soil by surface evaporation or through plants growing in the soil, Drainage represents the amount of water moving below the root zone, and Storage represents the amount of water stored in the soil root zone.
In this software the water balance is calculated on a daily basis. Historical daily rainfall amounts along with user-specified irrigation strategies are used to estimate infiltration. Potential evapotranspiration amounts calculated from historical weather data along with time dependent crop coefficients are used to estimate evapotranspiration. The soil water-holding capacity and known storage amount on a specific date are used to characterize the water stored in the soil. If the amount of water entering the soil on a particular day can be stored in the root zone, the drainage amount is zero for that day. If the infiltration exceeds the storage capacity of the soil the excess is lost as drainage.
Although the water balance concept is useful for some management purposes, it greatly simplifies the flow process and is not suitable for all uses. Clearly the model is not capable of providing information for time steps of less than one day. Also the model ignores soil water dynamics. It treats the infiltration, storage, and drainage processes as essentially instantaneous processes. This may lead to underestimating water storage and overestimating drainage. Another simplification in this model is the assumption that all rainfall enters the soil. Runoff is ignored. This too will tend to overestimate drainage.
In addition to simplifications in the model, we have uncertainty because we do not know the future weather distributions. Thus we cannot estimate the future water balance with certainty. To help overcome this problem, the applet allows the user to view predictions based on a number of past weather records. By viewing predictions collectively for all of these years, the user can gain an understanding of the possible range of predictions that may occur in the future. In more advanced models, more weather records are used and results are presented as probability distributions.
Root zone water balance during a specified period of time may be expressed as ( Hillel, 1998 )
![]()
where DS is the change in root-zone soil-moisture storage, DV is the amount of water incorporated in vegetative biomass, P is the amount of precipitation, I is the amount of irrigation water applied, U is the amount of water moved upward into the root zone by capillary flow, R is the amount of runoff per unit area, D is the amount of downward drainage out of the root zone, E the amount of evaporation from the soil surface, and Tr is the amount of water transpired by plants.
If the infiltration capacity of a soil system is large relative to rainfall intensities, no surface runoff will occur. If the depth to groundwater is large, the upward capillary flow into the root zone will be negligible. Neglecting surface runoff, upward movement of water from below the root zone, and the amount of water incorporated in vegetative biomass, the root-zone water balance in a soil system can be expressed as
![]()
where ET = E + Tr is the evapotranspiration. Evapotranspiration is frequently calculated from a reference evapotranspiration (Guyot, 1998; Hess, 1996) using the equation
![]()
where ET0 is the reference evapotranspiration from a reference canopy, such as 0.12-m-high grass for short crops or 0.5-m-high alfalfa for tall crops (Allen, 2000; Walter et al., 2000); Kcrop a dimensionless crop factor or crop coefficient reflecting the relative evapotranspiration of a crop of interest to that of a reference canopy, and Ksoil a dimensionless soil factor reflecting the fraction of water holding capacity that is readily available to the evapotranspiration process.
In this program, root zone water balance is calculated on a daily basis. The following equation can be used for daily water balance computation.
![]()
where Si and Si-1 are amounts of water stored in the root zone at the end of day i and day i-1, respectively. Pi, Ii, Di, and ETi represent precipitation, irrigation, drainage, and evapotranspiration amounts on day i. The water storage amounts must be greater than or equal to zero and less than or equal to the maximum amount of water that can be stored in the root zone, Smax.
The ability of a soil to conduct water is reduced as the soil dries out. At some point, the soil can no longer provide water to the plant roots at a rate sufficient to maintain plant turgor and wilting occurs. Eventually this condition can lead to permanent wilting of the plants. If we let Swilt represent the amount of water in the root zone when permanent wilting occurs, the amount of water available for plant use on day i, AWi, is given by
![]()
Combining equations 4 and 5 and treating the infiltration, storage, and drainage as essentially instantaneous processes, the available water on day i, AWi, can be calculated using the equation
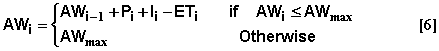
and the drainage amount on day i, Di can be calculated from the equation
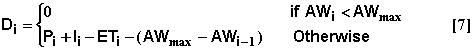
where AWmax is the water holding capacity.
Assumptions and Simplifications
1. The model ignores soil water dynamics. It treats the infiltration, storage, and drainage processes as essentially instantaneous processes.
2. All rainfall and irrigation water enters the soil. Runoff is ignored.
3. No water is carried upward into the root zone from the below.
4. Water intercepted by the vegetative biomass is insignificant.
Crop Coefficient: Crop coefficient is a dimensionless crop factor or coefficient reflecting the relative evapotranspiration of a crop of interest to that of a reference canopy.
Reference Evapotranspiration: Reference evapotranspiration represents evapotranspiration from a reference canopy (0.12-m-high grass for short crops or 0.5-m-high alfalfa for tall crops) under optimal soil-moisture conditions.
Soil Factor: Soil factor is a dimensionless soil factor reflecting the fraction of available water capacity that is readily available to plants.
Water Holding Capacity: Water holding capacity refers to the maximum amount of water in a root zone that is available to plant growth.
Bibliography
Allen, R. G. 2000. Using the FAO-56 dual crop coefficient method over an irrigated regions as part of an evapotranspiration intercomparison study. J. Hydrology 229:27-41.
Guyot, G. 1998. Physics of the environment and climate. John Wiley & Sons, Inc., 605 Third Avenue, New York, NY 10158-0012.
Hess, T. 1996. A microcomputer scheduling program for supplementary irrigation. p. 59-68. In M. Smith, L. S. Pereira, J. Berengena, J. Goussard, R. Ragab, L. Tollefson, and P van Hofwegen (ed.) Irrigation scheduling: From theory to practice. Proceedings of the ICID/FAO workshop on irrigation scheduling. International Commission on Irrigation and Drainage, Food and Agriculture Organization of The United Nations, Rome, Italy.
Hillel, D. 1998. Environmental Soil Physics. Academic Press, Inc. 525 B Street, Suit 1900, San Diego, CA 92101-4495.
Walter, I. A., R. G. Allen, R. Elliott, B. Mecham, M. E. Jensen, D. Itenfisu, T. A. Howell, R. Snyder, P. Brown, S. Echings, T. Spofford, M. Hattendorf, R. H. Cuenca, J. L. Wright, and D. Martin. 2000. ASCE's standardized reference evapotranspiration equation. Proceedings of the 4th National Irrigation Symposium, ASAE, St. Joseph, MI.
Contributors
This program was designed by Dr. D. L. Nofziger and Dr. J.Wu, Department of Plant and Soil Sciences, Oklahoma State University, Stillwater, OK 74078.
Send email to david.nofziger@okstate.edu
Last Modified: January 16, 2008.