Convective-Dispersive Transport with Steady-State Water Flow: Theory
General Description Model Description Simplifications Glossary Bibliography and Contributors
Convective-Dispersive Transport
Miscible displacement of a solute in soil solutions is simulated by the convection dispersion equation (CDE). For an absorptive, degradable, and transformable chemicals, the CDE may include terms of adsorption, degradation, and transformation. Van Genuchten and Alves (1982) developed analytical solutions to this equation for solute transport in one-dimensional semi-infinite soils with uniform initial conditions, and steady-state water flow. Two of their analytical solutions have been incorporated into this software. The model user can select the problem of interest and specify the parameters of the flow system. The software then displays graphs of concentration as a function of distance for selected times or concentration as a function of time for selected positions. By changing the input parameters, a user can observe changes in the concentration distributions and thus gain insight into the sensitivity of the transport process to each model parameter.
Governing Partial Differential Equation: One-dimensional, miscible displacement of an absorptive and degradable chemical species through a soil column of constant water content and flux is simulated by
![]()
where C = C(x,t) is the concentration at location x and time t; D=a L|v| is the dispersion coefficient; a L is the dispersivity; v=q/q is the pore water velocity; q is the volumetric water content; q is flux density of soil water (or the Darcy velocity); R=1+r Kd/q is the retardation factor; r is the soil bulk density; Kd is the partition coefficient; m is the first-order decay constant; and g is the zero-order production rate constant.
Two analytical solutions of van Genuchten and Alves (1982) are included in this software. The initial and boundary conditions for those problems are given below.
Initial condition: The concentration of chemical at all positions in the soil at time zero is a constant and equal to Ci. That is
![]()
Boundary condition: Two boundary conditions are supported.
1. In the first case, the concentration of chemical at the position x = 0 is specified for a period of time. Following that time, the concentration at the surface is zero. That is
![]()
where Co is the specified concentration at x = 0 and to is the duration of time for which this concentration is imposed.
2. In the second case, the concentration of chemical in the solution entering the soil system at the position x = 0 is specified for a period of time. Following that time, the concentration of chemical in the solution entering the system is zero. Mathematically, that is
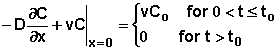
where Co is the concentration of the inflowing solution from time zero to time to.
Solutions: The analytical solutions for these flow problems are given in van Genuchten and Alves (1982).
Assumptions and Simplifications
1. The pore water velocity is a constant in time and space. This condition can be met for a uniform soil if the flux density of water (or Darcy velocity) and the volumetric water content are constant for all positions and all times.
2. The spreading of solutes dominated by hydraulic dispersion rather than diffusion.
3. The hydrodynamic dispersion can be approximated as the product of the dispersivity and pore water velocity
4. The adsorption process is instantaneous and reversible and the adsorption isotherm can be described by the linear model. That is, the concentration of chemical adsorbed on the soil solids is proportional to the concentration in solution, the adsorption reaction reaches equilibrium very quickly, and a reduction in solution concentration results in immediate desorption of the chemical from the soil solids.
5. The degradation reactions in both the liquid and solid phases obey first-order kinetics.
6. The production rate obeys zero-order kinetics in both solution and sorbed phases.
7. Soil and chemical parameters in the model are not dependent upon position in the soil or time.
Adsorption Isotherm: Adsorption isotherm refers to the functional relationship between the content of a chemical species in the adsorbed phase or retained by a absorbing solid and the concentration of that chemical in the bathing gas or solution phase that is at equilibrium with the adsorbing solid.
Darcy Velocity: Darcy velocity is the volume of water flowing through a unit cross-sectional area per unit time. It is a continuum-approach parameter. In a porous medium the cross-sectional area includes both the portion occupied by the flowing liquid and the portion occupied by solid and air.
Dispersivity: Dispersivity is a geometrical proportionality constant of a porous medium. It is determined by the pore-size distribution of the channels participating in the transmission of a bulk solution. It measures the spreading of a solute across the "front" of an average bulk flow.
First-order kinetics: First-order kinetics refers to a reaction process of which the reaction rate (usually represented by the decrease rate of a component reactant) is proportional to a concentration of the component reactant. The proportionality constant is called the first-order rate constant. In a degradation reaction, the first-order rate constant is also referred to as the first-order decay constant.
Hydraulic dispersion: Hydraulic dispersion refers to the spreading of a tracer due to the velocity variation in individual pores.
Hydrodynamic dispersion: Hydrodynamic dispersion refers to the spreading of a tracer beyond the region expected according to the average flow alone. It is the macroscopic outcome of the actual movements of individual tracer particles through the pores and the various physical and chemical phenomena that take place within the pores. Hydrodynamic dispersion includes hydraulic dispersion and molecular diffusion.
Miscible displacement: Miscible displacement refers to the movement of two or more completely soluble fluids in a porous medium. In this case, the interfacial tension between any pair of fluids is zero, and all the fluids dissolve in each other. In groundwater hydrology, this type of flow is referred to as hydrodynamic dispersion.
Molecular diffusion: The net transfer of mass (of a chemical species) by random molecular motion. This net mass transfer is usually caused by gradients in concentrations of a chemical species.
Partition coefficient: Partition coefficient is a proportionality constant in an equilibrium adsorption isotherm. It is the ratio of adsorbed content to the concentration in an aqueous solution for the linear equilibrium isotherm.
Pore water velocity: Pore water velocity refers to the average velocity inside soil pores. It may be calculated from Darcy velocity using v=q/q, where v is pore velocity, q is Darcy velocity, q is water content.
Retardation factor: Retardation factor is a dimensionless parameter characterizing the retarding effect of adsorption on solute transport. Mathematically, the retardation factor, R, is defined as R=1+rKd/q, where r is bulk density, Kd is partition coefficient, and q is volumetric water content.
Zero-order kinetics: Zero-order kinetics refers to a reaction process of which the reaction rate is independent of the concentrations of the reactants. The constant reaction rate is called zero-order rate constant. If the reaction rate measures the increase rate of the product of a reaction, the zero-order rate constant is also referred to as the zero-order production rate constant.
Bear, J. 1972. Dynamics of fluids in porous media. Dover Publications, Inc., New York.
Incropera, F. P. and D. P. DeWitt, 1990. Fundamentals of heat and mass transfer. John Wiley & Sons, Inc., New York.
Kotz, J. C. and K. F. Purcell, 1991. Chemistry and chemical reactivity. Saunders College Publishing, a division of Holt, Rinehart and Winston, Inc., Orlando, FL 32887.
Marshall T. J. and J. W. Holmes, 1988. Soil physics. Cambridge University Press, 32 East 57th Street, New York, NY 10022.
McBride, M. B., 1994. Environmental chemistry of soils. Oxford University Press, Inc., New York.
Nofziger, D.L., K. Rajender, Sivaram K. Nayudu, and Pei-Yao Su, 1989.CHEMFLO---One-dimensional water and chemical movement in soils. Agricultural Experiment Station, Division of Agriculture, Oklahoma State University, Stillwater, OK 74078.
van Genuchten M. Th. And W. J. Alves, 1982. Analytical solutions of the one-dimensional convective-dispersive solute transport equation. USDA ARS Technical Bulletin Number 1661. U.S. Salinity Laboratory, 4500 Glenwood Drive, Riverside, CA 92501.
Contributors
This program was designed by Dr. D. L. Nofziger and Dr. J. Wu, Department of Plant and Soil Sciences, Oklahoma State University, Stillwater, OK 74078.
Send email to dln@okstate.edu
Last Modified: Dec 11, 2001.