Water Movement in Soils
| Introduction: Water movement in soils is quite simple and easy to understand in some ways and quite complex and difficult to grasp in others. An object that is free to move tends to move spontaneously from a state of higher potential energy to one of lower potential energy. So it is with water. A unit volume or mass of water tends to move from an area of higher potential energy to one of lower potential energy. | |
|
|
|
| What gives rise to differences in
potential energy of a unit of water in a soil? The force of
gravity is one factor. Just as water at a higher elevation on a
street tends to run down to a lower elevation due to gravity, so water
in a soil tends to move downward due gravity. A second factor is the
attraction of the soil surfaces for water. When water is added
to the bottom of a dry pot of soil, the water moves up into the soil
due to this attraction of the soil surfaces for water. The energy level
of the water in contact with the soil particles is less than that of
the pool of water in the pan so it moves up into the soil. As the soil
in the pot becomes wet, this attraction is reduced so that by the time
the pores are completely filled, the soil no longer attracts additional
water. If a soil is saturated, a third source of potential energy can
exist in the form of external pressure such as that provided by
a pump or a layer of water in a flooded area. These are the main
sources of potential energy in soilwater. Other forms can exist, but
they will not be discussed here.
Direction of Water Movement: The total potential energy of water is the sum of the potentials from all sources. Potential energy per unit mass or per unit volume or per unit weight is known as the potential of the water. So water free to move will move from a region where it has higher total potential to one of lower total potential. The potential due to gravity is known as the gravitational potential and that due to the soil particles is the matric potential. Soils whose pores are not filled have matric potentials less than zero. Saturated soils under the influence of external hydrostatic pressures have matric potentials which are greater than zero. The total potential at any point is just the sum of the gravitational and matric (or pressure) potentials at that point. The distribution of total potential within a soil allows us to determine if water will move and the direction of movement for any soil system. If the total potentials are equal, no movement will occur. Details about water potential and how it can be determined in soils are available here. Rate of Water Movement: The section above introduces water potential and the manner in which it can be used to determine the direction of water movement. In this section, we will examine factors that determine the rate of movement. It is useful to think of water movement as the product of a driving force causing water to move and a factor representing the ease with which water moves in the soil. This was formalized by Henry Darcy in 1856 as
where q is the volume of water flowing through a unit cross-sectional area of soil per unit time, K is the saturated hydraulic conductivity of the soil, TH is the total hydraulic head and x is the position coordinate in the direction of flow. This equation is known as Darcy's Law. For uniform saturated soils, it is useful to write this equation as
where THA is the total head at the inlet end of the soil, THB is the total head at the outlet end of the soil column, and LAB is the distance between the inlet and outlet. The hydraulic conductivity, K, represents the ease with which water flows through a soil. Its value depends upon the soil properties and the properties of the soil water. The driving force, df, is represented by
Hydraulic Conductivity: Since some of the volume of a soil is occupied by soil particles, water does not flow through a soil as easily as it does through an open pipe. The ease of water movement is known as the hydraulic conductivity of the soil. Soils with large pores such as sandy soils tend to conduct water more easily than soils with smaller pores such as clay soils. Thus sands have higher saturated conductivity values than clays (Examples). As soils dry out, water in the largest pores is lost first. Water movement must then occur through smaller pores and in films near soil particles. These pores and films present more resistance so the conductivity of a soil decreases as it dries out (Examples). In nature the wetness of the soil often changes with position in the soil. Thus, the conductivity changes with position as well. Driving Force: The rate of water movement in soils increases with increasing driving force. In saturated soils the driving force is a result in differences in elevation and positive external pressures in the soil. In unsaturated soils, the attraction of the soil surfaces for water is often a major component to the driving force. Driving forces are commonly much larger in unsaturated soils than in saturated soils. The driving force commonly changes in magnitude with changing soil properties and wetness. Examples of this are available here. For more insight into driving forces in soils under one-dimensional steady-state flow, utilize the Steady-state Water Movement software and associated exercises. |
|
|
The following sections introduce dynamic flow processes that occur in nature. The CHEMFLO-2000 software can be used to simulate most of these transient processes. The mathematical model, computational methods, and suggested numerical experiments are included in the software manual. |
|
|
Infiltration: The process of water entering the soil
surface is known as infiltration.
Infiltration Rate: Infiltration is a very dynamic process. Water applied to the surface of a relatively dry soil infiltrates quickly due to the affinity of the soil particles for water. As time passes and the soil becomes wet, the force of gravity becomes the dominant force causing water to move. The infiltration rate gradually decreases with time and approaches the value of the saturated conductivity of the soil as shown at the right. This example is for the Cobb sandy loam in Caddo County Oklahoma. |
|
| Cumulative Infiltration: We are often interested in the total amount of water entering a soil. The graph at the right shows this cumulative infiltration as a function of time for the Cobb soil. The cumulative infiltration increases rapidly at small times and then approaches a linear relationship as the infiltration rate approaches a constant value. | |
| Water Content Distributions: When water enters a relatively dry soil from a flooded condition such as that used above, water at the inlet quickly approaches the saturated water content. The water content changes from its initial low value to a value near saturation in a small distance. As time passes this wetting front moves downward through the soil as shown at the right. The rate at which the wet front advances decreases with time and depth of wetting. In this example, the wetting front advanced about 25 cm in the first 4 hour period, 13 cm in the second period, and 10 cm in the fourth period. | |
| If water is applied at a lower rate so that ponding
does not occur, the infiltration rate, cumulative infiltration and
water content distributions change somewhat. For example, if the
application rate is 0.5 cm/hr (which is less than the saturated
conductivity of the soil), the infiltration rate is constant at 0.5
cm/hr for all times, the cumulative infiltration is a straight line
through the origin with a slope of 0.5 cm/hr, and the water content
distributions are shown at the right. Note that the water content at
the soil surface increases with time for the first 10 hours. Also the
wet front has not advanced as far as at the case of flooding. Finally,
the curves are not as steep (or wetting zone is larger) here as they
were under flooded conditions.
Many other factors influence the shape of these infiltration functions. They include the manner in which the unsaturated conductivity changes with water content or matric potential, the initial water content distribution in the soil, and changes in soil hydraulic properties with depth or time. |
|
|
|
|
|
Redistribution: The section above deals only with
the infiltration process. What happens when water is no longer applied
at the surface? Will water movement stop?
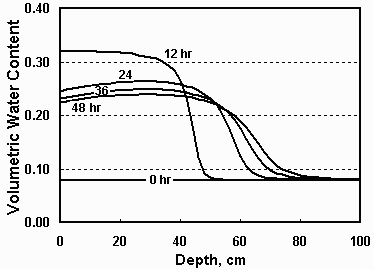
Clearly the answer is no. Forces which were present to cause water to move are still present. Those forces will continue to move water. The difference is that in order to wet the soil deeper in the profile, water must now be removed from upper wet regions. The figure at the right shows the predicted distributions of water at three times during redistribution (no water enters or leaves the soil surface during this time). Infiltration stopped at 12 hours. At 24, 36, and 48 hours, the water contents near the surface decrease and the wet front advances down the profile. The advance of the wet front is much slower than while water was being applied. The rate of advance and the rate of drying of the surface soil both decrease with time. This redistribution will continue, but at slower and slower rates. Because the rates decrease rapidly with time, soils have the ability to store water for plant use. |
 |
|
|
|
|
Evaporation: We know that water which is free to move moves from regions of higher potential to lower potential. The sources of potential for unsaturated soils are primarily the attraction of soil surfaces for water and the force of gravity. Water movement is not limited to downward movement nor to movement in the liquid phase. Evaporation from the soil surface can be large as well. Evaporation of water requires that water be present in the soil at the evaporation site. It also requires a substantial source of energy to convert liquid water to a vapor. Without that energy, evaporation cannot occur. Finally, sustained evaporation requires that the water vapor above the evaporation site must be moved away from that site. If that does not occur, the air becomes saturated with water so evaporation stops. Soon after infiltration, the soil surface is wet so plenty of water is available at the surface. In this early stage, the atmospheric demand or energy available to convert water to vapor are most likely to limit the evaporation rate. As the soil dries out, the ability of the soil to move water upward to the soil surface limits the evaporation rate. |
|
|
|
|
|
Plant Uptake: Water moves from soil to plant roots and on through plants as a result of potential differences, just as it does elsewhere. Water potentials in plants and the conductivity of the plant parts change rapidly and vary over large magnitudes depending upon the atmospheric conditions and the physiology of the plant. Plants are capable of removing large quantities of water from soils. Details at the microscopic scale of individual roots is difficult to study, but this basic work is being carried out. For most water management purposes, it is sufficient to quantify the average rate of water loss per unit area. This is often called the evapotranspiration rate or ET since it combines direct evaporation from the soil surface and evaporation of water taken up by plants and transpired through the plant system. Numerous methods have been developed to measure and estimate these evapotranspiration rates. Potential evapotranspiration rates or PET values are generally calculated for a reference crop growing under well watered conditions. ET values for a specific crop are obtained by multiplying this PET value by a crop coefficient to account for differences in plant species and stage of growth and by a soil factor reflecting differences in soil wetness and hence the soil potential and conductivity in the vicinity of the roots. |
|
|
|
|
|
Drainage: Water moving below the root zone of the plant is available to move the chemical deeper into the profile and to recharge the underlying aquifer. This amount depends upon the soils ability to store water, the evapotranspiration of the area, and the amount of water infiltrating the soil from rainfall or irrigation. An interactive program is available to examine this in more detail. |
|